Hi guys,
I wanted to share with you a solution widely used in shooting mechanics. In a friendly way I will tell you the conclusions I have reached, just to share some reflections.
Recently I was trying to convert the following instructions of a game demo created with Unity, from C# to java.
public Vector3 GetShotDirectionWithinSpread(Transform shootTransform)
{
float spreadAngleRatio = bulletSpreadAngle / 180f;
Vector3 spreadWorldDirection = Vector3.Slerp(shootTransform.forward, UnityEngine.Random.insideUnitSphere, spreadAngleRatio);
return spreadWorldDirection;
}
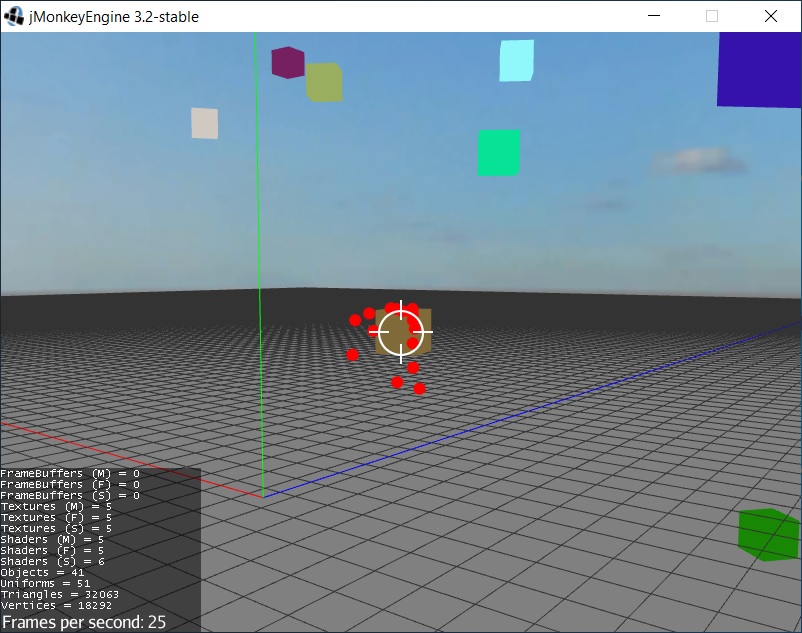
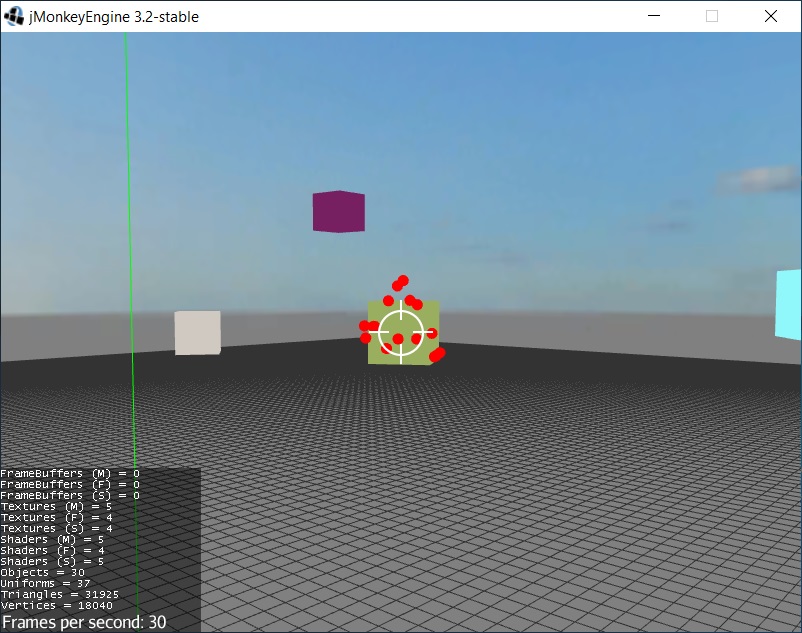
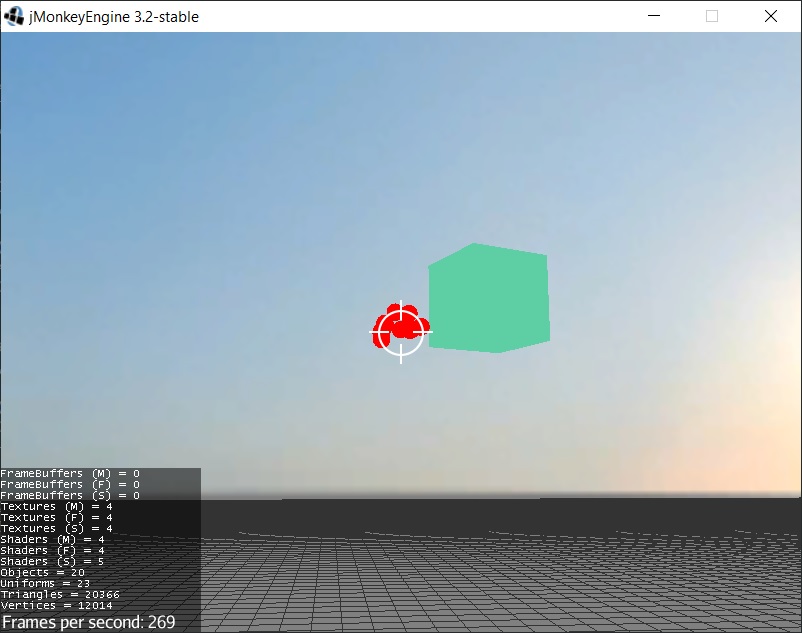
The code is used to generate random variations in the trajectory of the bullets. Used a lot to model the damage caused by shotgun ammunition.
I noticed that the Vector3f class does not contain two functions that I often encounter in Unity tutorials:
- Vector3.slerp
Unity - Scripting API: Vector3.Slerp - Random.insideUnitSphere
Unity - Scripting API: Random.insideUnitSphere
After some research I found that the math behind it is quite complex, but the Vector3 class of the libgdx library already contained a good implementation of these functions, so I adapted them with the objects of our JMonkeyEngine.
from libgdx:
/** Spherically interpolates between this vector and the target vector by alpha which is in the range [0,1]. The result is
* stored in this vector.
*
* @param target The target vector
* @param alpha The interpolation coefficient
* @return This vector for chaining. */
public Vector3 slerp (final Vector3 target, float alpha) {
final float dot = dot(target);
// If the inputs are too close for comfort, simply linearly interpolate.
if (dot > 0.9995 || dot < -0.9995) return lerp(target, alpha);
// theta0 = angle between input vectors
final float theta0 = (float)Math.acos(dot);
// theta = angle between this vector and result
final float theta = theta0 * alpha;
final float st = (float)Math.sin(theta);
final float tx = target.x - x * dot;
final float ty = target.y - y * dot;
final float tz = target.z - z * dot;
final float l2 = tx * tx + ty * ty + tz * tz;
final float dl = st * ((l2 < 0.0001f) ? 1f : 1f / (float)Math.sqrt(l2));
return scl((float)Math.cos(theta)).add(tx * dl, ty * dl, tz * dl).nor();
}
/** Sets the components from the given spherical coordinate
* @param azimuthalAngle The angle between x-axis in radians [0, 2pi]
* @param polarAngle The angle between z-axis in radians [0, pi]
* @return This vector for chaining */
public Vector3 setFromSpherical (float azimuthalAngle, float polarAngle) {
float cosPolar = MathUtils.cos(polarAngle);
float sinPolar = MathUtils.sin(polarAngle);
float cosAzim = MathUtils.cos(azimuthalAngle);
float sinAzim = MathUtils.sin(azimuthalAngle);
return this.set(cosAzim * sinPolar, sinAzim * sinPolar, cosPolar);
}
@Override
public Vector3 setToRandomDirection () {
float u = MathUtils.random();
float v = MathUtils.random();
float theta = MathUtils.PI2 * u; // azimuthal angle
float phi = (float)Math.acos(2f * v - 1f); // polar angle
return this.setFromSpherical(theta, phi);
}
to jme3:
public class FVector {
/**
* Spherically interpolates between start vector and the end vector by
* alpha which is in the range [0,1].
*
* @param start The start vector
* @param end The end vector
* @param alpha The interpolation coefficient
* @return The result vector
*/
public static Vector3f slerp(final Vector3f start, final Vector3f end, float alpha) {
final float dot = start.dot(end);
// If the inputs are too close for comfort, simply linearly interpolate.
if (dot > 0.9995 || dot < -0.9995) {
return new Vector3f().interpolateLocal(start, end, alpha);
}
// theta0 = angle between input vectors
final float theta0 = (float) Math.acos(dot);
// theta = angle between this vector and result
final float theta = theta0 * alpha;
final float st = (float) Math.sin(theta);
final float tx = end.x - start.x * dot;
final float ty = end.y - start.y * dot;
final float tz = end.z - start.z * dot;
final float l2 = tx * tx + ty * ty + tz * tz;
final float dl = st * ((l2 < 0.0001f) ? 1f : 1f / (float) Math.sqrt(l2));
return start.scaleAdd((float) Math.cos(theta), new Vector3f(tx * dl, ty * dl, tz * dl)).normalizeLocal();
}
/**
* Sets the components from the given spherical coordinate
*
* @param azimuthalAngle The angle between x-axis in radians [0, 2pi]
* @param polarAngle The angle between z-axis in radians [0, pi]
* @return This vector for chaining
*/
public static Vector3f setFromSpherical(float azimuthalAngle, float polarAngle) {
float cosPolar = FastMath.cos(polarAngle);
float sinPolar = FastMath.sin(polarAngle);
float cosAzim = FastMath.cos(azimuthalAngle);
float sinAzim = FastMath.sin(azimuthalAngle);
return new Vector3f(cosAzim * sinPolar, sinAzim * sinPolar, cosPolar);
}
public static Vector3f insideUnitSphere() {
float u = FastMath.nextRandomFloat();
float v = FastMath.nextRandomFloat();
float theta = FastMath.TWO_PI * u; // azimuthal angle
float phi = (float) Math.acos(2f * v - 1f); // polar angle
return setFromSpherical(theta, phi);
}
}
Here is the final result. I hope my story will be useful to you. Let me know if I have made any mistakes or if there are simpler functions that I may not have found.
public class Main {
...
private Shotgun weapon;
private Node bulletNodeGroup;
private Geometry bulletGeo;
@Override
public void onAction(String name, boolean isPressed, float tpf) {
if (name.equals("shooting") && isPressed) {
shooting();
}
}
private void shooting() {
Vector3f origin = cam.getLocation();
for (int i = 0; i < weapon.bulletsPerShot; i++) {
Vector3f shotDirection = weapon.getShotDirectionWithinSpread(cam.getDirection());
Spatial g = instantiate(bulletGeo, origin, Quaternion.IDENTITY, bulletNodeGroup);
g.addControl(new BulletControl(bulletAppState, origin, shotDirection));
}
}
private void initBulletPrefab() {
Sphere sphere = new Sphere(32, 32, .05f);
bulletGeo = new Geometry("Bullet.GeoMesh", sphere);
Material mat = new Material(assetManager, "Common/MatDefs/Misc/Unshaded.j3md");
mat.setColor("Color", ColorRGBA.Red);
bulletGeo.setMaterial(mat);
}
private Spatial instantiate(Spatial model, Vector3f position, Quaternion rotation, Node parent) {
Spatial sp = model.clone();
sp.setLocalTranslation(position);
sp.setLocalRotation(rotation);
parent.attachChild(sp);
return sp;
}
...
}
public class Shotgun extends IWeapon {
...
// Angle for the cone in which the bullets will be shot randomly (0 means no spread at all)
float bulletSpreadAngle = 5f;
// Amount of bullets per shot
int bulletsPerShot = 10;
public Vector3f getShotDirectionWithinSpread(Vector3f shotDirection) {
float spreadAngleRatio = bulletSpreadAngle / 180f;
Vector3f spreadWorldDirection = FVector.slerp(shotDirection, FVector.insideUnitSphere(), spreadAngleRatio);
return spreadWorldDirection;
}
...
}