So I take it I wasn’t supposed to use perlin noise to get the random offset? 
 I think you summoned Cthulhu
I think you summoned Cthulhu

For the random offset i use this texture

(released into Public Domain)
i sample it at vec2(g_Time*factor,0.);
Thanks! One step closer, though I had to use a mod(g_Time,1.0) otherwise the image stayed the same color. Also had this odd problem where the distortion only applied itself to the bottom left quarter of the screen. What exactly does the GPU do when the texcoords exceed the range from 0.0 to 1.0?
Depends on the texture wrap mode, if set to REPEAT for both axes ( texture.setWrap(WrapMode.Repeat) in jme ) it will repeat itself. I think you have it set to clamp (that’s probably why you need mod(g_Time,1.0) ).
Remember that the value you read from the texture is always positive, if you want to make it random in all directions you have to move the interval between [-1;1] : color.rgb * 2. - 1.
:chimpanzee_facepalm: Yes exactly lol.
I totaly forgot wrap modes existed.
Yes, see other thread on the basic network example.
How advanced is that system? Are the orbits stable?
The thing is, if you’re just adding the black hole’s force vector to the planet every update the orbit won’t be here for a long time. Floating point errors will punch it out of whack soon.
The way to counter that is to calculate the orbital path as a conical function and use that for all future updates. At least that’s what KSP does.
For the interested reader, i.e. the interested computer games programmer that wants to get closer to reality:
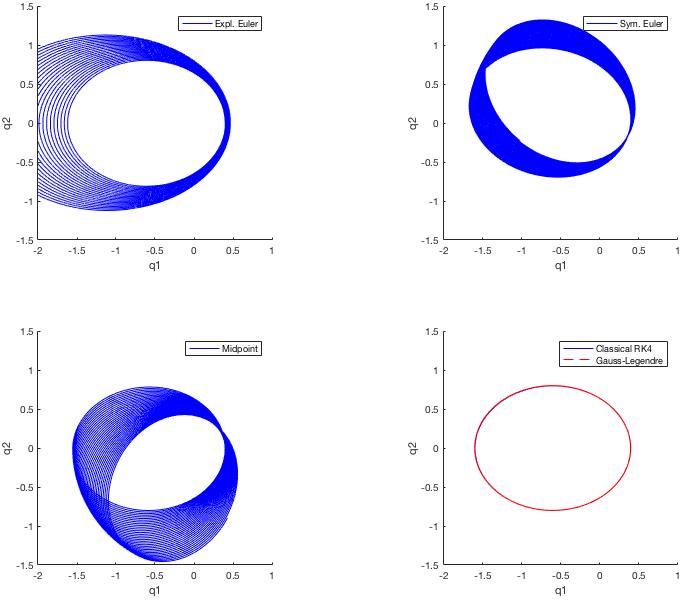
Actually this is not the main problem. Distances are large and floating point numbers have a precision of 7 digits! But when integrating the equations of motion numerically, you will probably run into problems depending on the method of integration. (here “integration” = solving over time). The most common approach in computer games is to calculate the acceleration from the force, add it to the velocity and add the velocity to the current position. This is known as the Explicit Euler Method, which typically increases the energy of a system (see image below). The reason is that the time step dt is not even close to zero, and we cannot make it arbitrary small because we would need to make more steps and hence decrease performance.
There are more advanced methods that take the change of the parameters over a time step dt better into account. For example I use a classical Runge-Kutta algorithm of order four for my flight simulator project. Though it looks exact for the Kepler problem, the energy decreases slightly. This is, because the phase space has four dimensions (two positions (x,y) and two velocities (v_x, v_y)).
I recently completed a project about numerical integration at the university, here are some results. This image shows the change of initial energy over time.
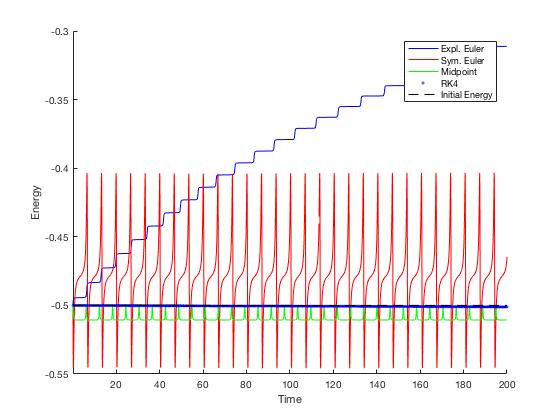
And the next image shows the orbital perturbation caused by the method of integration. The symplectic Euler method preserves energy, but there is some sort of angular pertubation, as in the Midpoint method. The naive Explicit Euler method increases energy, as explained above. The Runge Kutta (RK4) and Gauss-Legendre methods are quite precise and almost overlap.
The thing with conical functions in KSP is nice, as it is an analytic solution to a two-body problem. But what if the spaceship enters the atmosphere? In this case the Explicit Euler method fails, if you want to come close to reality. ![]()
@MoffKalast, it is not advanced at all, I just applied jbullet’s .setGravity and .applyForce at the right time. For some dark reasons, the orbit never stops. It is really weird and I have not yet figured out why.
Also, for what the program knows, there is no orbit. The ‘orbit’ you see is just the effect of the 2 functions mentioned above, thus making it dynamic (?). Adding other forces completely changes the orbit. Thus, there is no orbital path or calculation, just physics.
@Apollo, thank you for the explanation, it is really helpful.
I was just horsing around with gravity and physics offered in jME, no big deal. However, if I’d do anything with gravity, space and orbits, I’d make it as realistic as possible (no paths, just gravity).
Does anyone know how well jME’s physics can handle this?
Hah! KSP circumvents the two body problem by making only one attractor affect your rocket at a time. When going to other planets you pass their spheres of influence and are only affected by them there.
If the rocket enters an atmosphere it’s back to all regular physics without any orbits. Not really an elegant solution.
@anon54790888 You haven’t made a new discovery in physics…
Not a dark reason, it’s just that you have a small area where precision is high and you aren’t observing the orbit for a long time. Eventually it will get altered in an unexpected way.
Yes, it’s an apparent emergent property of the system. It seems really cool and all at first, but it doesn’t work quite as well as you’d expect.
I’m telling you all this because I made something simmilar in 2D when I was still messing around with JavaFX. It worked in the exact same way and calculated forces for all bodies in the scene, but the fact that I was just adding up forces made it inaccurate in the long term.
http://i.imgur.com/JCbfqTO.png
Which is what we’ve just explained, you can’t do because of floating point number limitations.
Go ahead though, but don’t be surprised when your ships start crashing into planets on their 300th orbit.
Well, I’m not 100 % sure about bullet physics, but I don’t expect any advanced integration method. It is most probably an Explicit Euler method. But you can test the stability of jbullet simply by plotting the path of your object over a long time scale. You can also store the position at each time step and use an external plot tool, like MS Excel. BTW: a different good stability test would be a numerical model of a pendulum, i.e. the harmonic oscillator.
However, if you ever want to have realistic orbital mechanics you should really use a representation other than floats, as @MoffKalast pointed out. But this is probably beyond bullet physics? To me, bullet physics are game-only physics, that make everything look great but it is far from a realistic model. Please correct me if I’m wrong.
I think it’s funny that in springer embedder style graph layouts, orbits and oscillations were exactly what we try to prevent. All along I could have told my users to just keep waiting! 
Bi-Directional language support for Lemur with TrueTypeFont
(Tested For Arabic and Persian)
Hope you like 
Poem is from Sa’adi
Persian :
Arabic Translation :
English Translation :
Unfortunately I do not understand any Persian or Arabic, so thank you for the translation. Btw, the letters are rendered very nicely.
‘It’ is now playable in its most basic form:
Clicking on a castle opens the radial selector (slick visuals I know), choose how many units to select, the click another castle to either attack, or reinforce.
Oh and the mouse cursor got screen captured in the wrong place, somehow.
Still very early, but promising.
Indeed.
@thetoucher, I love the look and style and where you are going with this.
Looking forward to more eye candy… 
Not as exciting as cool visualizations… but I’m working on documentation. Yes, aren’t you jealous?!?
Here is the latest iteration of the SimEthereal overview diagram showing the major working parts and how they would interact with user code:
Don’t know if it makes sense to anyone else but it makes sense to me! 
Hey those mechanics look simmilar to that mobile game I used to play, Biotix. But there your viruses don’t fight other viruses so it’s a bit lamer. More stuff to capture though.
So the server handles all physics for everyone? I guess that is the best way to guarantee synchronisation, but what about muh performance?