Hexagonal Terrain Mesh

[anon54790888]

Hi everyone.

I have a board (Set<Tile>) of hexagonal tiles. Currently, I’m drawing them one by one. As this is draining fps quite fast, I want to improve the way I draw them. The best way is to make a large mesh (and use LOD/chunks if it gets big), just like a normal terrain.
I thought (and found examples) of at least three different possibilities to make such terrain, and I decided to start with the simplest, which does not use hexagonal voxels:

• If two tiles are next to each other, but at different heights, it draws a wall to connect them
• If two tiles are next to each other, and at the same height, the vertexes should be re-used (no overlapping vertexes in the vertex buffer)
• If no neighbor is found, and the tile is at height >0, a wall should go to height=0 (so you don’t have large gaps in the side of your map)

This is what is it should look like (although this uses hex voxels):

Does anyone have any code/mesh/examples that I can use or learn from?

UPDATE:
I made a prototype of the algorithm in another language (open scad) to show how it would aproximatly look like:

As you can see, all tiles are at different heights, and walls connect to them. However, I did not add the walls at the outside (or the re-use of vertices, but you can’t see that in this picture).

[jayfella]

Have you seen this?

https://jmonkeyengine.github.io/wiki/jme3/advanced/custom_meshes.html

[anon54790888]

@jayfella

Have you seen this?

Yes.

I’m not asking “how do you make a custom meshes in jME”, I’m asking “can anyone help me making this specific mesh”. I know how to make custom meshes, but I don’t want to reinvent the wheel making this kind of hexagonal terrain.

[jayfella]

Well there is this… (set the point selection to hex)

http://www-cs-students.stanford.edu/~amitp/game-programming/polygon-map-generation/demo.html

It has a link where he/she describes the algorythm. I have played around with hexagons myself, but it seemed so wasteful (the top of a hexagon alone needs 5 triangles vs 2 for a cube) so I didnt venture much further than the basics.

EDIT: and he also has the source on git.

amitp/mapgen2

[pspeed]

I mean, to me, the general algorithm is the same as for cubes.

for each hexagon
-for each side of the hexagon
–if side is visible, emit quad

Where “side is visible” is defined as hex next to me in that direction is lower than me.

Which of that seems trickiest?

[anon54790888]

Alright I just went for it:

This uses jME and actual tile objects (not just mock-up data). The only things I did not manage to do were the the walls on the outside. I have a question about them:

The code I used assumed all vertexes were already in place, and only searches them. However, the outside walls need to create at most 2 new vertices. What’s the best way of finding out that a vertex already exists (i.e. no two same vertices int the vertex buffer)?
Here’s a picture to explain (the white dot should only be created once):

[thetoucher]

Make sure you actually want to be sharing vertices, generally shared verts = smooth shading, which you will not want on all of your edges; The only place you should be sharing verts is on the same face (n.b. this rule applies to flat shaded meshes).

Later down the track if you make your terrain editable, if you do have shared verts, the process of adding and removing cells can become a nightmare and a lot more complicated than needs be, trust me

[thetoucher]

@anon54790888

What’s the best way of finding out that a vertex already exists (i.e. no two same vertices int the vertex buffer)?

When I created hex tiles, during creating I stored many internal lookups (arrays and maps) of things like “HexCellToVerts” and “HexCellToFaces” to facilitated easy lookups. Remember to make your data work for you, keeping a good organised internal model and having useful utility methods (such as: getThe8NeighbouringTiles(), isThereASolidNeighbourAt() and getAllVertsForTile) will make mesh creating that much easier.

Figuring out vertices from the buffers during creation is like trying to debug you application from the complied java code rather than looking at the source.

[pspeed]

@anon54790888

The code I used assumed all vertexes were already in place, and only searches them.

This is not a good idea. Unless you really want that weird smoothness then you want each quad to have its own vertexes. vertex = position + normal + texture coordinate, etc… all shared.

[anon54790888]

@pspeed

vertex = position + normal + texture coordinate, etc… all shared

@thetoucher

if you do have shared verts, the process of adding and removing cells can become a nightmare

This makes sense.

@thetoucher

I stored many internal lookups (arrays and maps)

I also figured that would be the easiest for me, so I’ll try to use more maps and arrays.

To conclude, I should

• Let every face have separate vertices, even when they overlap
• Use maps, arrays, lists, etc. to make my life easier

I will try it!
Thanks for the advice.

[anon54790888]

UPDATE:

This is the complete terrain. Now I just need to add textures. I will post the source in a few days.

[janvonpichowski]

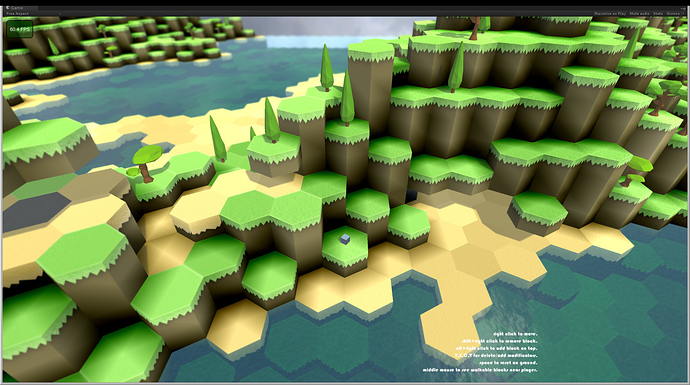
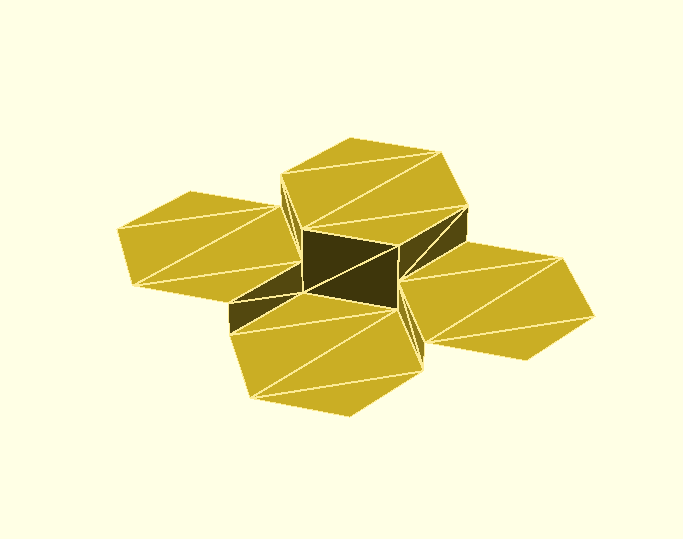
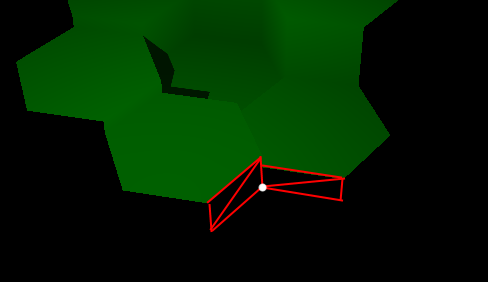
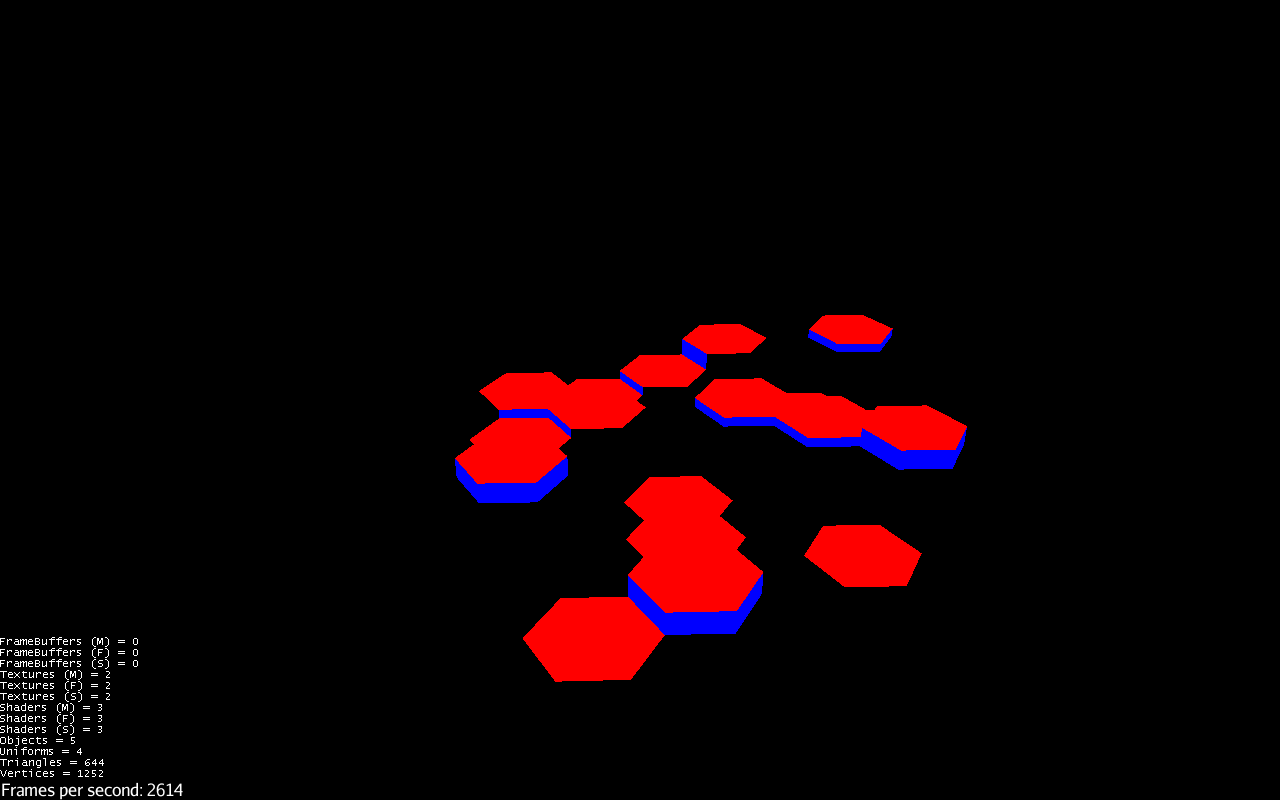
This is how I did it once (don’t mind the fps without vsync it is around 3000):

package com.jvpichowski.hex;

import com.jme3.app.SimpleApplication;
import com.jme3.material.Material;
import com.jme3.math.Vector2f;
import com.jme3.math.Vector3f;
import com.jme3.scene.Geometry;
import com.jme3.scene.Mesh;
import com.jme3.scene.Node;
import com.jme3.scene.VertexBuffer;
import com.jme3.util.BufferUtils;
import jme3tools.optimize.GeometryBatchFactory;

/**
 * 
 */
public class HexTest extends SimpleApplication {

    private final float size = 0.5f;
    private final float width = size * 2;
    private final float horiz = width * 3/4;
    private final float height = 0.25f;

    public static void main(String[] args) {
        new HexTest().start();
    }

    @Override
    public void simpleInitApp() {
        Node root = getRootNode();
        addHex(root, 1, new int[]{0,0,2,4,6,0},  new Vector3f(0.75f*width,0,0.5f*horiz));
        addHex(root, 2, new int[]{0,0,0,3,4,1},  new Vector3f(0,0, horiz));
        addHex(root, 3, new int[]{2,0,0,0,4,4},  new Vector3f(-0.75f*width,0,0.5f*horiz));
        addHex(root, 4, new int[]{4,3,0,0,0,5},  new Vector3f(-0.75f*width,0,-0.5f*horiz));
        addHex(root, 5, new int[]{6,4,4,0,0,0},  new Vector3f(0,0,-horiz));
        addHex(root, 6, new int[]{0,1,4,5,0,0},  new Vector3f(0.75f*width,0,-0.5f*horiz));
        addHex(root, 4, new int[]{1,2,3,4,5,6},  new Vector3f(0,0,0));
        GeometryBatchFactory.optimize(root);
    }

    private void addHex(Node node, int center, int[] borders, Vector3f location){
        Material mat = new Material(assetManager, "Common/MatDefs/Misc/Unshaded.j3md");  // create a simple material
        //mat.setColor("Color", ColorRGBA.Blue);   // set color of material to blue
        mat.setTexture("ColorMap", assetManager.loadTexture("Hex.png"));
        //mat.getAdditionalRenderState().setFaceCullMode(RenderState.FaceCullMode.Off);
        location = location.add(0, height*center, 0);

        Vector3f[] vertices = new Vector3f[6];
        vertices[0] = new Vector3f(0.5f*width, 0f,0f);
        vertices[1] = new Vector3f(0.25f*width, 0f,0.5f*horiz);
        vertices[2] = new Vector3f(-0.25f*width, 0f,0.5f*horiz);
        vertices[3] = new Vector3f(-0.5f*width, 0f,0f);
        vertices[4] = new Vector3f(-0.25f*width, 0f,-0.5f*horiz);
        vertices[5] = new Vector3f(0.25f*width, 0f,-0.5f*horiz);

        Vector2f[] texCords = new Vector2f[6];
        texCords[0] = new Vector2f((0.5f+0.5f)/2, 1-(0.5f+0)/2);
        texCords[1] = new Vector2f((0.5f+0.25f)/2, 1-(0.5f+0.5f)/2);
        texCords[2] = new Vector2f((0.5f-0.25f)/2, 1-(0.5f+0.5f)/2);
        texCords[3] = new Vector2f((0.5f-0.5f)/2, 1-(0.5f+0)/2);
        texCords[4] = new Vector2f((0.5f-0.25f)/2, 1-(0.5f-0.5f)/2);
        texCords[5] = new Vector2f((0.5f+0.25f)/2, 1-(0.5f-0.5f)/2);

        int[] indices = {
                5, 1, 0,
                5, 4, 1,
                4, 2, 1,
                4, 3, 2
        };

        Mesh hex = new Mesh();
        hex.setBuffer(VertexBuffer.Type.Position, 3, BufferUtils.createFloatBuffer(vertices));
        hex.setBuffer(VertexBuffer.Type.TexCoord, 2, BufferUtils.createFloatBuffer(texCords));
        hex.setBuffer(VertexBuffer.Type.Index, 3, BufferUtils.createIntBuffer(indices));
        hex.updateBound();

        Geometry hexGeom = new Geometry("", hex);
        hexGeom.setLocalTranslation(location);
        hexGeom.setMaterial(mat);                   // set the cube's material
        node.attachChild(hexGeom);

        for(int i = 0; i < borders.length; i++) {
            if (borders[i] == center-1) {
                Vector3f[] vertices1 = new Vector3f[4];
                vertices1[0] = vertices[i].clone();
                vertices1[1] = vertices[(i+1)%6].clone();
                vertices1[2] = vertices[i].add(0, -height, 0);
                vertices1[3] = vertices[(i+1)%6].add(0, -height, 0);

                int[] indices1 = {
                        0, 3, 2,
                        3, 0, 1
                };

                Vector2f[] texCords1 = new Vector2f[6];
                texCords1[0] = new Vector2f(0f/2, 0.5f);
                texCords1[1] = new Vector2f(1f/2, 0.5f);
                texCords1[2] = new Vector2f(0f/2, 0);
                texCords1[3] = new Vector2f(1f/2, 0);

                Mesh s1 = new Mesh();
                s1.setBuffer(VertexBuffer.Type.Position, 3, BufferUtils.createFloatBuffer(vertices1));
                s1.setBuffer(VertexBuffer.Type.TexCoord, 2, BufferUtils.createFloatBuffer(texCords1));
                s1.setBuffer(VertexBuffer.Type.Index, 3, BufferUtils.createIntBuffer(indices1));

                Geometry s1Geom = new Geometry("", s1);
                s1Geom.setMaterial(mat);
                s1Geom.setLocalTranslation(location);
                node.attachChild(s1Geom);

            }else if (borders[i] < center-1){
                Vector3f[] vertices1 = new Vector3f[6];
                vertices1[0] = vertices[i].clone();
                vertices1[1] = vertices[(i+1)%6].clone();
                vertices1[2] = vertices[i].add(0, -height, 0);
                vertices1[3] = vertices[(i+1)%6].add(0, -height, 0);
                vertices1[4] = vertices[i].add(0, -height*(center-borders[i]), 0);
                vertices1[5] = vertices[(i+1)%6].add(0, -height*(center-borders[i]), 0);

                Vector2f[] texCords1 = new Vector2f[6];
                texCords1[0] = new Vector2f(0f/2, 0.5f);
                texCords1[1] = new Vector2f(1f/2, 0.5f);
                texCords1[2] = new Vector2f(0f/2, 0);
                texCords1[3] = new Vector2f(1f/2, 0);
                texCords1[4] = new Vector2f(1f/2, 0);
                texCords1[5] = new Vector2f(1f/2, 0);

                int[] indices1 = {
                        0, 3, 2,
                        3, 0, 1,
                        2, 3, 5,
                        5, 4, 2
                };

                Mesh s1 = new Mesh();
                s1.setBuffer(VertexBuffer.Type.Position, 3, BufferUtils.createFloatBuffer(vertices1));
                s1.setBuffer(VertexBuffer.Type.TexCoord, 2, BufferUtils.createFloatBuffer(texCords1));
                s1.setBuffer(VertexBuffer.Type.Index, 3, BufferUtils.createIntBuffer(indices1));

                Geometry s1Geom = new Geometry("", s1);
                s1Geom.setMaterial(mat);
                s1Geom.setLocalTranslation(location);
                node.attachChild(s1Geom);
            }
        }
    }
}